Italian translation at settesei.it
Rafael Nadal won Indian Wells. Roger Federer won on the blue clay. Even Alessio Di Mauro won a match on a hard court last week.
That’s just a sliver of the anecdotal evidence for one of the most common complaints about contemporary ATP tennis: Surface speeds are converging. Hard courts used to play faster, allowing for more variety in the game and providing more opportunities to different types of players. Or so the story goes.
This debate skipped the stage of determining whether the convergence is actually happening. The media has moved straight to the more controversial subject of whether it should. (Coincidentally, it’s easier to churn out columns about the latter.)
We can test these things, and we’re going to in a minute. First, it’s important to clarify what exactly we mean by surface speed, and what we can and cannot learn about it from traditional match statistics.
There are many factors that contribute to how fast a tennis ball moves through the air (altitude, humidity, ball type) and many that affect the nature of the bounce (all of the same, plus surface). If you’re actually on court, hitting balls, you’ll notice a lot of details: how high the ball is bouncing, how fast it seems to come off of your opponent’s racket, how the surface and the atmosphere are affecting spin, and more. Hawkeye allows us to quantify some of those things, but the available data is very limited.
While things like ball bounce and shot speed can be quantified, they haven’t been tracked for long enough to help us here. We’re stuck with the same old stats — aces, serve percentages, break points, and so on.
Thus, when we talk about “surface speed” or “court speed,” we’re not just talking about the immediate physical characteristics of the concrete, lawn, or dirt. Instead, we’re referring to how the surface–together with the weather, the altitude, the balls, and a handful of other minor factors–affects play. I can’t tell you whether balls bounced faster on hard courts in 2012 than in 1992. But I can tell you that players hit about 25% more aces.
Quantifying the convergence
In what follows, we’ll use two stats: ace rate and break rate. When courts play faster, there are more aces and fewer breaks of serve. The slower the court, the more the advantage swings to the returner, limiting free points on serve and increasing the frequency of service breaks.
To compare hard courts to clay courts, I looked for instances where the same pair of players faced off during the same year on both surfaces. There are plenty–about 100 such pairs for each of the last dozen years, and about 80 per year before that, back to 1991. Focusing on these head-to-heads prevents us from giving too much weight to players who play almost exclusively on one surface. Andy Roddick helped increase the ace rate and decrease the break rate on hard courts for years, but he barely influences the clay court numbers, since he skipped so many of those tournaments.
Thus, we’re comparing apples to apples, like the matches this year between David Ferrer and Fabio Fognini. On clay, Ferrer aced Fognini only once per hundred service points; on hard, he did so six times as often. Any one matchup could be misleading, but combine 100 of them and you have something worth looking at. (This methodology, unfortunately, precludes measuring grass-court speed. There simply aren’t enough matches on grass to give us a reliable sample.)
Aggregate all the clay court matches and all the hard court matches, and you have overall numbers that can be compared. For instance, in 2012, service breaks accounted for 22.0% of these games on clay, against 20.5% of games on hard. Divide one by the other, and we can see that the clay-court break rate is 7.4% higher than its hard-court counterpart.
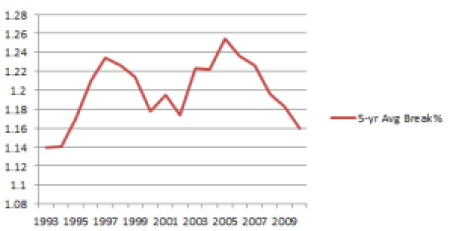
That’s one of the smallest differences of the last 20 years, but it’s far from the whole story. Run the same algorithm for every season back to 1991 (the extent of available stats), and you have everything from a 2.8% difference in 2002 to a 32.8% difference in 2003. Smooth the outliers by calculating five-year moving averages, and you get finally get something a bit more meaningful:
The larger the difference, the bigger the difference between hard and clay courts. The most extreme five-year period in this span was 2003-07, when there were 25.4% more breaks on clay courts than on hard courts. There has been a steady decline since then (to 16.9% for 2008-12), but not to as low a point as the early 90s (14.0% for 1991-1996), and only a bit lower than the turn of the century (17.8% for 1998-2002). These numbers hardly identify the good old days when men were men and hard courts were hard.
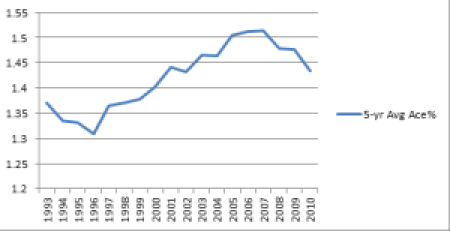
When we turn to ace rate, the trend provides even less support for the surface-convergence theory. Here are the same 5-year averages, representing the difference between hard-court ace rate and clay-court ace rate:
Here again, the most diverse results occurred during the 5-year span from 2003 to 2007, when hard-court aces were 51.3% higher than clay-court aces. Since then, the difference has fallen to 46%, still a relatively large gap, one that only occurred in two single years before 2003.
If surfaces are converging, why is there a bigger difference in aces now than there was 10, 15, or 20 years ago? Why don’t we see hard-court break rates getting any closer to clay-court break rates?
However fast or high balls are bouncing off of today’s tennis surfaces, courts just aren’t playing any less diversely than they used to. In the last 20 years, the game has changed in any number of ways, some of which can make hard-court matches look like clay-court contests and vice versa. But with the profiles of clay and hard courts relatively unchanged over the last 20 years, it’s time for pundits to find something else to complain about.
It would be interesting (though awfully laborious) to survey articles from the past year or so about convergence & glean as many solid quotes as possible (that is, quotes not taken out of context) from the players themselves. If players repeatedly question or complain about a phenomenon of some sort, there must be *something* to it; the question is, what exactly?
It would be nice to know what players have said. I do think that this topic is driven as much by the media as by the players, and now it has become close enough to conventional wisdom that players don’t have to think critically about it.
IMO, it’s just that players are stronger and (especially) faster, and better rackets amplify both of those things, meaning that any player is able to chase more balls down *and* stay in rallies longer than the equivalent player could 10 or 20 years ago. The Novak-ification of the ATP. The resulting game looks more like clay-court tennis than hard-court tennis, even when 1 in 10 serves is an ace.
Very true. Maybe they need to speed up the courts due to the shear athleticism of the players today. All I know if that tournaments like Indian wells and Miami look like they are being played on clay as it is near impossible to hit through the court. Did you see the Murray, Ferrer final? That was not hard court tennis the was it was meant to be played. Who wants to watch that.
Great post.
Sent from my Verizon Wireless BlackBerry
Players are faster and taller and poly string also help with returns. If you want to look at data you have to look at average rally, winners, etc. You can’t just look at serves. There is no doubt they have put more sand in the courts, so it’s stupid to say that the hard courts have not slowed down.
It’s stupid?
Looking forward to seeing your proof.
Such a flawed method of testing! For what it’s worth the number of aces and breaks in itself today can be attributed to a number of factors and are NOT exclusively surface-oriented. All I needed was to read the parameter you’ve set for your so-called testing to know your post was nonsensical. And where is your proof that aces and breaks alone determine surface speeds. You show that and then ask others for proof.
What are those factors?
What other available stats would you use?
The friction of the ball with the surface, on contact, height of the player serving, etc. The mere fact that you can ace more on HC doesn’t make them fast. In fact the highest number of aces in a single match (50 ) occured a few years ago at Roland Garros on clay. Are we to assume RG plays fast then? No. Hard Court is a plain surface, leaving a greater likelihood for the ball to slide off than clay. That however, will not prevent the surface from being slower if you are to take into account the entirety of a given match, the speed at which the ball travels through the Court, the bounce, etc. The best method of a gauging that is to simply gauge the way players approach the game and what they think of the surfaces. Because there is no meter of surface speeds known to me at least. But then, I’m not the one writing an article and inviting comments on it either. 😉
I think one problem here is something that economist Dylan Evans has pointed to in his writings about risk assessment: namely, that verbal labels for complex phenomena are inherently susceptible to varying interpretation – so much so that they make agreement nearly impossible. And the problem is not necessarily solved by creating a mathematical measure (that is, a probability) for a given label – because people will *still* insist on interpreting the label differently (often without being aware of what they are doing), and thus will interpret what the probability “means” in very different ways.
To get pedantic for a moment, the example Evans uses is that the Intergovernmental Panel on Climate Change has stated in reports on global warming that it uses the label “unlikely” to refer to events with have an estimated probability of less than 33 percent, and “very likely” to refer to events with an estimated probability of at least 90 percent. But research elsewhere (e.g. a study in 2009 in the journal “Psychological Science” showed that some persons privately interpret the label “unlikely” as including events with as much as a 66 percent probability – twice the threshold intended by the Panel on Climate Change.
So back to tennis – it appears we have some readers who dispute the use of math to explore court speed by saying they disagree with the very notion that math can even be used for this purpose – they assert that the phenomenon is simply too complex. I suspect the real problem here is that such readers are as bad at math as I am, but don’t want to admit it! And on the other hand, more usefully, we have readers who more reasonably suggest that ace count isn’t enough & that other data should be collected.
This gives me an idea. Obviously some data simply aren’t available that might be useful. But . . . if someone who was good at math had infinite time and personal access to players at least at the challenger level or better . . . it seems to me there would be a way to generate useful additional data anyway, as follows: First, select a group of challenger-or-better players who would be willing to be interviewed periodically about their experience after playing a particular court. This could be done several times during the year so as to collect data on X many different court compositions. The interviews would need to be done *immediately* after the player concluded a match on a given surface, so that their recollections would be fresh. The interview technique would be similar to that espoused by expert knowledge researcher Gary Klein (“Sources of Power,” etc.). The goal of the interview would be to first illicit whether the player considered the surface in question to be fast, slow, medium, or what have you – after which the interviewer would ask open-ended questions about what the player’s actual *experience* was that suggested this fastness or slowness. After this, the researcher could see what data might be linked to the verbal labels that had been expounded on in such detail.
For example, we might find that a low bounce height is closely married to a player’s subjective impression of fastness. We might speculate that a low bounce takes away reaction time during rallies and when returning as well. But the key would be to see if the data for this metric matched up with the extended verbal descriptions from the players. Etc. etc.
I meant to add that even data like “bounce height” are not really singular, but packages – i.e. not just the court but the type of ball & the weather will affect “bounce height.” That introduces some slop into the data that are actually available.
But more pertinently, it seems to me that a limitation with numerical analysis will always be that complex phenomena – i.e. any event in the natural world – can never, in the end, truly be unpacked into discrete events. A comparison is how we speak about water: if we measure by atom count, we might be tempted to say that hydrogen is more responsible for making up water than is oxygen. But if we measured by molecular weights, we might be tempted to say that really, oxygen is more important to a water molecule, since it outweighs the hydrogen. But the fact is, for many discussions, such attempts at dissection into separate components are not useful for understanding “water” as we experience it.
So too, the questions about court speed are much more entangled than our wording sometimes suggests. “Speed” is not something a court possesses in isolation. It might be more appropriate to talk of “how fast a court ‘plays’,” with the emphasis on the verb (“plays”) since verbs are much more suggestive of the interplay involved.
Is it possible that for years when the hard courts are significantly faster, there would be less pairs on the faster courts since they are unlikely to meet compared to when hard courts are slower. Like for example, pairs are unlikely to meet at Cincinnati because they are to fast and different to clay but are instead likely to meet at Miami because it is similar. Would this affect the result since if there are significantly less pairs on the faster courts, the results would be skewed by the slower had courts.
Is it possible that court speed was about the same until about 2007, and that the increase in aces and breaks was generated by better racket/string technology, and perhaps other factors like fitness, technique, but since 2007 courts have been slowed down which has led to a reduction in the aces and breaks on hard vs clay.
That seems to fit. I would argue than by eye we can clearly see that some hard courts surfaces were just faster in 2000-2006 than they are today.Certainly either balls or courts, and probably at least in part courts.
Not sure if better racket/string technology could generate both more aces and more breaks at the same time – but it could be possible – the decline of ability to win points at the net overcompensating any advantage gained by aces.
In this theory the strings and other factors could cause marginal gains on hard up to 2007 of aces and breaks would not make much difference on clay because of the nature of the game there.